Structural combinations of the 4 ccp lattices

Structural combinations of the 4 ccp lattices

These structural combinations can be of the same or different atoms and of the same or different sizes. In the presentation to follow all atoms are at the vertices, and all vertices are occupied. This becomes an alternative system to identifying unit cells.

1. The four ccp lattices: A, B, C, or D.

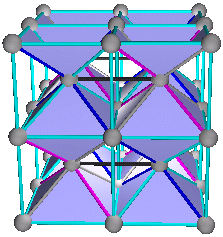
2. Combinations of A+B or C+D are the Simple Cubic (sc) structure or NaCl type structure. All of each others octahedra voids are filled. We have octahedral coordination, which is the alternative unit cells for simple cubic. A+B and C+D are two distinct simple cubic lattices that are topologically the same.

3. Combinations of A+C, B+C, A+D, or B+D are the cubic Diamond and related structures or ZnS structure. Half of each others tetrahedra are filled, A fills the negative tetrahedra of C and C fills the positive tetrahedra of A. We have tetrahedral coordination. There are four distinct diamond lattices that are topologically the same.

4. Combinations of A+(C+D), B+(C+D), (A+B)+C or (A+B)+D are the fluorite (AX2) CaF2 and the antifluorite (A2X) Na2O structures. Half of the (C+D) simple cubic are filled or all of A's or B's tetrahedra are filled, and half of the (A+B) simple cubic are filled or all of C's or D's tetrahedra are filled. It can also be seen as two interpenetrating diamond lattices like A+(C+D) as combination of diamond lattices (A+C) and (A+D).

5. Combinations of A+B+C+D are the body centered cubic structure. All tetrahedra and octahedra are filled, or (A+B)+(C+D) the CsCl structure (two simple cubic), (A+C)+(B+D) or (A+D)+(B+C) viewed as two interpenetrating diamond structures.

---

1. The Cubic Closest Packed Structure
A, B, C, or D

Elements: Al, Ca, Cu, Ni, Sr, Rh, Pd, Ag, (Ce), (Tb), Ir, Pt, Au, Pb, Th
See (Fig.5a, 5b, 5c, or 5d)

Compounds: Cu3Au, AlNi3 (others?). See (Fig. 20b) under Compound ccp lattice (Cu3Au)

---

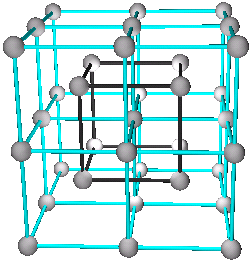
2. The Simple Cubic Structure or NaCl Structure
A+B or C+D

Elements: Alpha Po

Compounds: NaCl, AgCl, BaS, CaO, CeSe, DyAs, GdN, KBr, LaP, LiCl, LiF, MgO, NaBr, NaF, NiO, PrBi, PuC, RbF, ScN, SrO, TbTe, UC, YN, YbO, ZrO (Ref. 4)

Fig. 6a. Combination A+B. 3 frequency simple cubic or 27 sc unit cells. A in red, and B in blue.



Fig. 6b. Combination C+D. 2f or 8 unit cells. C in red, and D in blue.

---

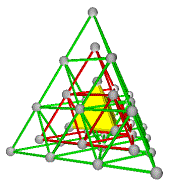
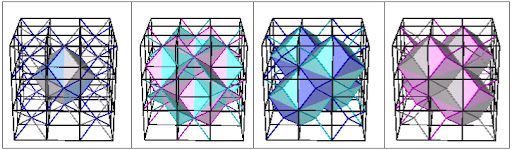
3. The Cubic Diamond Structure or ZnS Structure
A+C, B+C, A+D, or B+D

Elements: C (diamond), Si, Ge, Sn (grey)

Compounds: ZnS, AgI, AlAs, AlP, AlSb, BAs, BN, BP, BeS, BeSe, BeTe, CdS, CuBr, CuCl, CuF, CuI, GaAs, GaP, GaSb, HgS, HgSe, HgTe, InAs, InP, MnS, MnSe, SiC, ZnSe, ZnTe (Ref. 4)



Fig. 7a. Combination A+C. Diamond net (blue) interconnecting the A and C lattices.


Fig. 7b. Combination B+C. Diamond interconnecting net not shown.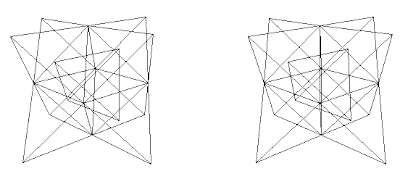





Fig. 7c. Combination A+D. Diamond interconnecting net in blue.

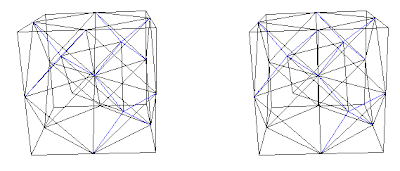
Fig. 7d. Combination B+D. Diamond interconnecting net in blue.

Fig. 7e. Diamond net, 4 unit cells. Traditional view. Combination A+C.

Fig. 7f. Diamond structure, same as (Fig. 7e). It is the combination A+C with A in blue. The interconnecting diamond net is not shown.

---

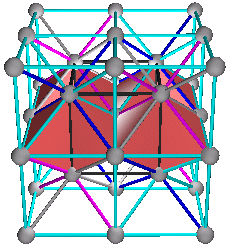
4. The Fluorite (AX2) and Antifluorite (A2X) Structures
A+(C+D), B+(C+D),
C+(A+B) or D+(A+B)

Elements: ? (There should be elements with this structure, unless this is an exception)

Compounds: CaF2,AmO2, AuAl2, AuIn2, BaF2, Be2B, CdF2, CeO2, CoSi2, EuF2, HgF2, Ir2P, Li2O, Na2O, NiSi2, PtAl2, Rb2O, SrCl2, SrCl2, SrF2, ThO2, ZrO2 (Ref. 4)





Fig. 8a. Traditional view of fluorite structures. CaF2 as shown on pg. 252 (Ref. 3) and pg. 52 (Ref. 5). This is a C+(A+B) combination, where Ca = (C) and F = (A+B) as shown in (Fig. 8b)





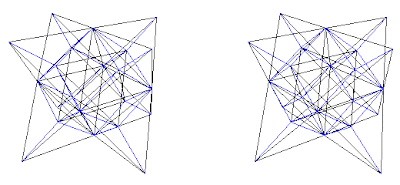
Fig. 8b. Combination C+(A+B). CaF2 shown in traditional view in blue with Ca = C lattice and F = (A+B) lattices. Cube outline is not shown.





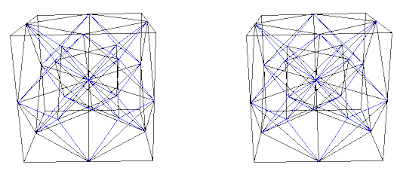
Fig. 8c. Combination D+(A+B) with interconnecting blue net.







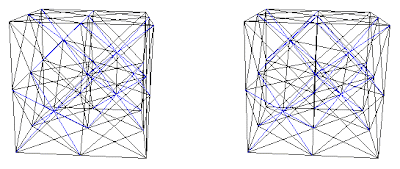
Fig. 8d. Combination A+(C+D) with interconnecting blue net.

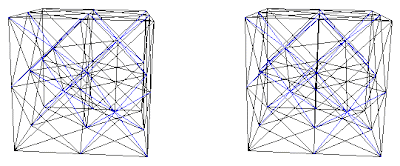
Fig. 8e. Combination B+(C+D) with interconnecting blue net.

Fig. 8f. Fluorite of 8 unit cells. They are cubic closest packed rhombic dodecahedra. This is a C+(A+B) view.

---

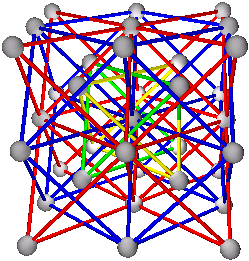
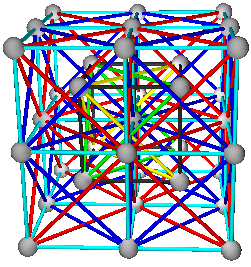
5. Body Centered Cubic Structures
A+B+C+D
(A+B)+(C+D)
(A+C)+(B+D) or (A+D)+(B+C)

Elements: W, Li, Na, K, V, Cr, Fe, Rb, Nb, Mo, Cs, Ba, Eu, Ta

Compounds:

• CsCl, CsBr, RbCl, AlCo, AgZn, BeCu, MgCe, RuAl, SrTl (Ref. 4)
• NaTl, LiZn, LiCd, LiAl, LiGa, NaIn, (pg 1301, Ref. 3)
• Fe3Al, Li3Bi, Li3Sb, Li3Pb, (pg 1301, Ref. 3)
• AlCu2Mn, AlNi2Ti, AlNi2Hf (Ref. 4)

CsCl has structure of type (A+B)+(C+D) with A=Cs, B=Cs, C=Cl, and D=Cl, or (Cs+Cs)+(Cl+Cl)






Fig. 9a. CsCl structure with traditional view.



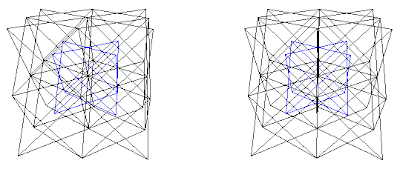
Fig. 9b. CsCl structure, (A+B)+(C+D). With (A+B) in blue.

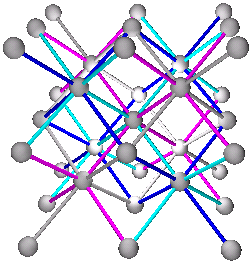
Fig. 9c. NaTl with combination of (A+B)+(C+D) as (Na+Tl)+(Tl+Na). Tl is shown in blue. Also shown is the partial tetrahedral axial view, or the two interpenetrating diamond view, or (A+C)+(B+D) view on the upper right corner.
The above is the same view as (Fig. 29.12), pg 1301 (Ref. 3).
The 2 interpenetrating diamond view of (A+C)+(B+D) (Ref. 4) or to view in 3D go to: The NaTl (B32) Structure

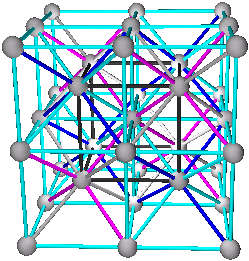
Fig. 9d. Fe3Al with combination of (A+B)+(C+D) as (Al+Fe)+(Fe+Fe) with Al shown in blue.
Same as shown in pg. 1298, fig. 29.10 (b) (Ref.3)

Cs3Sb has the same structure as Fe3Al with ((Cs/Sb)+Cs)+((Cs/Sb)+Cs) where (Cs/Sb) are equal numbers of Cs and Sb occupying sites A and C at random. From pg. 1301, (Ref. 3).

I just realized that the above coincides with Table 29.7, Structures of the CsCl-NaTl family, pg. 1302 (Ref. 3), in a way the atom positions Wells identified as A, B, C, and D corresponds exactly to the lattices A, B, C, and D used here. His chart includes in addition: Li3Bi, Bi2OF4, NaY3F10. Li3Bi shown in chart as A=Bi, B=Li, C=Li, D=Li it would translate to (A+B)+(C+D) as (Bi+Li)+(Li+Li) same as (Fig. 9d), Bi2OF4 shown in chart as A=4 Bi, (B,C,D)=2 O + 8 F, is not sufficient information to translate. NaY3F10 shown in chart as A=Na, 3 Y, (B, C, D)=10 F, from fig. 9.7, pg 422, translates to (A+B)+(C+D) as ((Na, 3 Y)+F)+(F+F) where Na occupies a tetrahedral vertex and 3 Y occupy the other three vertices of the tetrahedron.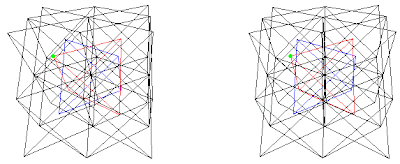






Fig. 9e. NaY₃F₁₀ in the combination (A+B)+(C+D) where Na in green and Y in red are A, F in blue is B, and F also occupy C and D lattices in black.





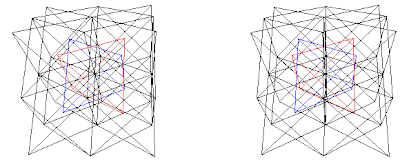
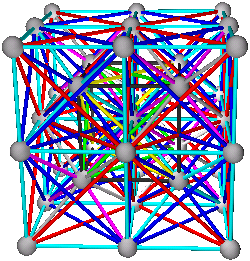
Fig. 9f. AlCu₂Mn (A+B)+(C+D) (Al+Mn)+(Cu+Cu), Al is red and Mn is blue, from (Ref. 4) or to view in 3D go to: The Heusler (L2₁) Structure

Evolution 1985-2003

Viewing Buckminsterfullerene as a Tensegrity Structure, Feb 23, 2003

Mapping the Hidden Patterns in Sphere Packing, Jan 2003

The ccp and hcp family of structures, Sept 1998

Introduction to Synergetic Crystallography,Feb 1998

Synergetica 1991 by Kirby Urner (last Synergetica)

Synergetica 1985 by Russell Chu (first Synergetica)

Bio Russ Z. Chu

The Pattern of Patterns

Structural combinations from 4 IVM (fcc) to Bcc lattices

from A, B, C, D to A+B+C+D

Last update 2-24-2003

(This is a Chart of the pattern of patterns)

I. Combinations of 4 IVMs (A, B, C, D)



[Combinations of 2, tetrahedral edges]
1a. 2 Cubic nets

A+B

AB+CD 2 interpenetrating cubic nets (bcc)

C+D





1b. 4 Diamond nets


A+C = AC

B+C = BC

A+D = AD

B+D = BD

[Combinations of 3, tetrahedral faces]

2. 4 Rhombic Dodecahedral nets ABC, ABD, ACD, BCD ivm (see II-1b below)


A+B+C = ABC

A+B+D = ABD

A+C+D = ACD

B+C+D = BCD


3. Combination of (I-1a), 2 cubic nets

AB+CD = 2 interpenetrating cubic nets = bcc lattice





II. Combinations of 4 Diamond nets (AC, BC, AD, BD) [I-1b]

[Combinations of 2]
1a. Two Interpenetrating Diamond nets

AC+BD

ACBD+BCAD 4 interpenetrating diamond nets (bcc)

BC+AD


1b. 4 Rhombic Dodecahedral nets (RD nets), (see I-2)

AC+BC = D’ RD net = ABC ivm

AD+BD = C’ RD net = ABD ivm

AC+AD = B’ RD net = ACD ivm

BC+BD = A’ RD net = BCD ivm


[Combinations of 3]
2. 4 Half-filled RD nets (of 3 diamond combinations)

AC+BC+BD = D’ RD net ½ filled by BD

AD+BD+AC = C’ RD net ½ filled by AC

AC+AD+BC = B’ RD net ½ filled by BC

BC+BD+AD = A’ RD net ½ filled by AD


3. Combination of (II-1a), 2 interpenetrating diamond nets

ACBD+BCAD = 4 interpenetrating diamond nets = bcc





III. Combinations of 4 RD nets (ACBC, ADBD, ACAD, BCBD) [II-1b]


[Combinations of 2]

1a. 2 Coupler nets


ACBC+ADBD = D’+C’= odd coupler

ACBC,ADBD+ACAD,BCBD =“Siamese Couplers”

=2 interpenetrating coupler nets = RITE net = (bcc)

ACAD+BCBD = B’+A’= even coupler





1b. 4 Half-filled RD nets (of 2 RD combinations), note the filling difference between III-1b and II-2

D’+B’ = ACBC+ACAD = D’ RD net ½ filled by AD

C’+A’ = ADBD+BCBD = C’ RD net ½ filled by BC

C’+B’ = ADBD+ACAD = B’ RD net ½ filled by BD

D’+A’ = ACBC+BCBD = A’ RD net ½ filled by AC




[Combinations of 3]
2. 4 Three RD nets (degenerated? into pairs of odd and even coupler nets)

A’B’C’ = BCBD+ACAD+ADBD = 2 interpenetrating RD, B’+A’= even coupler net (ADBD is redundant)

A’B’D’ = BCBD+ACAD+ACBC = 2 interpenetrating RD, B’+A’= even coupler net

A’C’D’ = BCBD+ADBD+ACBC = 2 interpenetrating RD, D’+C’= odd coupler net

B’C’D’ = ACAD+ADBD+ACBC = 2 interpenetrating RD, D’+C’= odd coupler net





3. Combination of (III-1a), 2 coupler nets

ACBC,ADBD+ACAD,BCBD = 2 interpenetrating coupler nets = RITE net = bcc





IV. Combinations of 4 Half Filled RD nets [III-1b]


1a.

1b.

2.

3.


I. Combinations of 4 IVMs (A, B, C, D)



[Combinations of 4]
3. Combination of all 4 IVMs

A+B+C+D = 4 IVM = bcc, including all the above pattern combinations.


Notes on main patterns:

• The various patterns obtained through the possible combinations of the 4 IVMs or 4 fcc lattices are limited between the fcc lattices and the bcc lattice.
• With 4 different lattices we can have a total combination of 6 pairs. And they are differentiated into two groups, group 1a with 2 combinations and 1b with 4 combinations.
• The 2 pairs in I-1a, II-1a, III-1a, are always complementary, and their combination lead directly to the final stage the bcc lattice.
• The 4 pairs in I-1b, II-1b, III-1b, are the new 4 lattices that can combine in the same way as the previous 4 lattices.
• I do not know if this repeating pattern goes on indefinitely, it appears that at III-2 we start seeing a redundancy where it suggest an end to the 4 pairs pattern. The 4 pairs become in essence 2 pairs due to redundancy.

Mapping the Hidden Patterns in Sphere Packing(4)

Mapping the Hidden Patterns in Sphere Packing

by Russell Z Chu




Combination of all 4 fcc lattices

This is the last combination. We started by identifying the 4 fcc lattices and showed all the possible combinations, the six combinations of 2 fcc lattices and the four combinations of 3 fcc lattices. This is the combination of all 4 fcc lattices, making a total of 11 combinations.

The combination of 4 interpenetrating fcc lattices or all of the fcc lattices together is the body center cubic lattice (bcc). It is the combination of the 4 fcc lattices with the 2 cubic nets and the 4 diamond nets or 4 rhombic dodecahedron nets, all together.



Different views of the bcc lattice




















Figure 24a. The 4 fcc lattices.

Figure 24b. The 2 cubic nets.






















Figure 25a. The 4 fcc lattices with the 2 interconnecting cubic nets.

Figure 25b. The 4 diamond nets or 4 interpenetrating rhombic dodecahedron nets.






















Figure 26a. The 2 cubic nets with the 4 diamond nets (which are the same as the 4 rhombic dodecahedral nets.)

Figure 26b. The body center cubic lattice with all of the 4 fcc lattices and the interconnecting nets.




















Figure 27a. The ‘coupler’ net is another possible view of the bcc lattice.

Figure 27b. This is one view of the ‘syte’ net.

Richard Hawkins has pointed out that Fig. 27b is one of the modules that Fuller named ‘SYTE’ (SYmetrical TEtrahedron) and that this particular syte is named ‘RITE’.

The coupler and syte are part of Fuller’s allspace-filling quanta module system. ”All the geometries in the cosmic hierarchy (see Table 982.62) emerge from the successive subdividing of the tetrahedron and its combined parts.” Synergetics 100.105.


The coupler is an asymmetrical octahedron. It is a 1/3 of the cube, which can be seen divided in 6 parts in fig. 26a by the 4 diagonals, or diamond nets.


The syte is an asymmetrical tetrahedron. It is a 1/4 of the coupler. Both couplers and sytes are considered ‘all space fillers’.





























Figure 28. The bcc lattice with 4 fcc lattices and all the interconnecting nets.



Overview and Conclusion

This exploration of the patterns in sphere packing was confined to the cubic closest packing branch and we only explored the growth of patterns from the face centered cubic (fcc) lattice to the body centered cubic (bcc) lattice. The evolution from fcc to bcc structures.

Most of the patterns exhibited here are known patterns, but often only partially observed.

In review, it became apparent that Fuller’s use of concentric pattern growth denoted in frequencies, in the isotropic vector matrix, was a key to facilitating my finding the 4 fcc lattices. I identified the other 3 fcc lattices from the growth patterns of the isotropic vector matrix which I labeled the cuboctahedral D fcc lattice.

The face center cubic (fcc) lattice, with emphasis on the 8 spheres at the corners of the cube and the 6 spheres at the center of the cubic faces (the octahedron), is the octahedral C lattice.

Only recently I learned that Richard Hawkins had identified 4 interpenetrating rhombic dodecahedral lattices from a different path. “I arrived at this understanding by realizing that one coupler can integrate either whole or half into six different rhombic dodecahedral domains in an RD packing and that since the domains on either side of the couplers 2 rhombic equators are part of the same lattice, there are four rhombic dodecahedral lattices in allspace.” R. Hawkins, 2003. You may view his work here.

It is heartening to see that others have come to the same conclusions from different paths.

We notice that different patterns of various combinations of fcc lattices, including the 4 fcc lattices correlate to known structural patterns of elemental and compound chemical structures. A hierarchy between the different patterns was established by showing that they could be derived from the associations of the 4 prime fcc lattices. This followed the order of the simpler to the complex by adding two, three, and 4 lattices together.

We note that in the evolutionary patterns from fcc structures to bcc structures (as shown in this paper) the original length between sphere centers of the fcc lattices remained the same. What this means is that the size of spheres decreased with each structural combination. If the sizes of spheres were to have remained the same the overall structure would have expanded, i.e. the packing would be less dense. In reality the combinations can be of different size atoms, or variations on the sizes of atoms such as a decrease in size due to added structural connections.

As proposed by Donald Ingber in “The Architecture of Life” we found that the underlying principle of tensegrity does extend to the assembly of atoms. That the new interconnections between the self-assembly of atoms, as in compound structures, work together with the original structural systems to form a new tensegrity system.

It is proposed by R. Chu that synergy could be associated with the added interconnections in the new compound structures, in particular, the new structural elements of the new tensegrity system. This was first shown in Fig. 15a.

The above implies that, in compound structures, the parts of the new system still maintain their original structural integrity. If this is true it would mean that some chemical elements, that exhibit compound patterns, would have differences between the atoms. I.e. diamond structures are composed of two fcc lattices, this could mean that there are two kinds of carbons, and bcc structures are composed of 4 fcc lattices, etc…

When we look at the structures of the chemical elements we find that the three most common structures are hcp, fcc, and bcc. From Table 1.1 of “Bonding and Structure of Molecules and Solids” by David Pettifor (1995), we find that, out of the 92 elements: 25 are hcp type, 20 are fcc type, 12 are bcc type, 3 are diamond type, one is simple cubic type, and 31 are of other types.

Towards the end of this exploration it became evident that there are many parallels with Fuller’s quanta modules, which are being explored by Richard Hawkins.

Further explorations of structural patterns derived from Fuller’s isotropic vector matrix could extend our knowledge of the evolution of structures.


January 21, 2003


______________________________________________________________________________________________

Previous Page Home Page Page 1, 2, 3 Next Page

Mapping the Hidden Patterns in Sphere Packing(3)

Previous Page Home Page Next Page

Mapping the Hidden Patterns in Sphere Packing

by Russell Z Chu


Combinations of 3 fcc lattices

There are four possible combinations of 3 fcc lattice connections. See section on Connections between 4 fcc lattices.



1. A+B+C
2. A+B+D
3. A+C+D
4. B+C+D


Due to the increased complexity of patterns, not all the lattices are being shown at the same time. I also tried enhancing some polyhedral faces with color. All of the patterns, shown in this paper, are taken from one single computer model separated into 1, 2, 3, and 4 frequency models. They all contain the following patterns in them, the 4 fcc lattices, the 2 cubic nets and the 4 diamond nets.

The rhombic dodecahedron nets, that we are going to see below, are combinations of 2 diamond nets. The two colors of the rhombic dodecahedron net are the same as the color of the diamond nets. See color below the color chart.

The color code used for lattices and nets:

The 4 fcc lattices:

• Tetrahedral A lattice (yellow)
• Tetrahedral B lattice (green)
• Octahedral C lattice (red)
• Cuboctahedral D lattice (blue)

The 2 cubic nets:

• Cubic AB net (black) from the A+B lattice combination.
• Cubic CD net (Aqua) from the C+D lattice combination.

The 4 diamond nets:

• Diamond AC net (blue) from the A+C lattice combination.
• Diamond BC net (gray) from the B+C lattice combination.
• Diamond AD net (aqua) from the A+D lattice combination.
• Diamond BD net (purple) from the B+D lattice combination.

The Rhombic Dodecahedron Net structural growth patterns
Also associated with Fluorite type structures.

Chart 4.


Figure 20a, 20b, 20c and 20d.





Figure 21a, 21b, 21c and 21d.



















Figure 22a, 22b.

Fig. 20a is showing the first possible rhombic dodecahedron. The rhombic dodecahedron is a compound structure. It takes three different fcc lattices to make a rhombic dodecahedron. As shown at top of Chart 4, it is a combination of A+B+C lattices. The two diamond nets are the blue AC net and the gray BC net. The diamond nets are the same as the diamond nets shown in the previous diamond net patterns.

In the first row of figures, only the rhombic dodecahedron nets are being shown. Not shown are the 3 fcc lattices and the other cubic net.

All 4 combinations shown above are rhombic dodecahedron nets. It becomes more apparent when looking at the second and third row. The first row is a 2 frequency cube grid, the second row is a 3 frequency cube and the third row is a 4 frequency cube.

In the first column, the combination A+B+C lattices has a rhombic dodecahedron at the center of the cube, which is the origin, the location of the first sphere of the D lattice. As the structure grows to the 4 frequency level there will be 12 more rhombic dodecahedrons, one attached to each face of the original rhombic dodecahedron. If this reminds you of the cuboctahedron you are right, it has the same orientation as the cuboctahedral D lattice.

Next in the combination A+B+D lattices there are six partial rhombic dodecahedron with their 4 edge corner sharing the origin. Note that in Fig. 21b the 6 partial rhombic dodecahedron’s openings are oriented towards the faces of the cube. They make the octahedron. They have the orientation of the octahedral C lattice.

The third combination of A+C+D is easier to see. There are 4 rhombic dodecahedrons, they make the shape of a tetrahedron. It is in the orientation of the tetrahedral B lattice.

In the last combination B+C+D it is also 4 rhombic dodecahedrons and this time it is in the tetrahedral A lattice orientation. It is possible to tell which tetrahedral orientation it has because I kept the orientation of the model the same throughout this project.

Some emerging patterns

The orientation pattern – if we look at the A+B+C lattice combination we see that the D lattice is missing and that happens to be the orientation pattern of the rhombic dodecahedrons. We have a rhombic dodecahedral net in the pattern of the cuboctahedral D fcc lattice. They are closest packing. The same follows for the other 3 combinations. We note that the rhombic dodecahedrons are empty. We will see next that in the last combination A+B+C+D that the D lattice will occupy the centers of the rhombic dodecahedral voids.

This is the 1st occurrence, in this system, of a polyhedron adopting the fcc lattice pattern. We know that others like icosahedrons and fullerenes can adopt the the structure of fcc pattern.

The rhombic dodecahedron net is the new set of repeating patterns of 4 fcc lattices.

Rhombic dodecahedron tensegrity





















Figure 23.

We are looking at the 3 fcc lattices A+B+C (yellow, green and red), the cube net (black), and the rhombic dodecahedral net (blue). Again this is a tensegrity structure and it is increasingly more complex. With each added layer there is an added web of connectivity. We can see how much information we are missing when we look at this structure as only a rhombic dodecahedral net or a cubic net.

January 21, 2003

______________________________________________________________________________________________

Previous Page Home Page Page 1, 2, 4 Next Page

Viewing Buckminsterfullerene as a Tensegrity Structure

Viewing Buckminsterfullerene as a Tensegrity Structure

by Russell Z Chu
February 23, 2003

The representation of the Buckminsterfullerene (Carbon 60) as a truncated icosahedron is structurally unstable. Likewise the cube is structurally unstable and it could be stabilized by introducing diagonal tensional elements at the faces or viewed as a compound structure of two tetrahedra with the cube as tensional elements.










I came to the understanding of Fullerene tensegrities from my research of crystalline structures in “Mapping the hidden patterns in sphere packing”. In this research I realized that a stable cubical structural system could be viewed as a tensegrity system. That there are secondary structural elements that account for stabilizing the primary unstable system.

With this understanding I decided to look at C60 for the secondary structural elements that would stabilize its primary truncated icosahedron structure.





















The figure above is a screen capture of a model built with SpringDance 3D program.

The primary structure of C60 in red color is what we are used to seeing, the truncated icosahedron.

The secondary structural elements are tensional elements. They are the yellow tension elements inside the pentagons and the aqua tensional elements inside the hexagons. These tensional elements are all the secondary connections from one carbon atom to the next nearest atom. The primary connections are the red truncated icosahedron.

This tensegrity system is similar to the bicycle wheel, but instead of spokes it is a spherical tensional net. The bouncy property of C60 can be attributed to the tensegrity structural system.