These structural combinations can be of the same or different atoms and of the same or different sizes. In the presentation to follow all atoms are at the vertices, and all vertices are occupied. This becomes an alternative system to identifying unit cells.
1. The four ccp lattices: A, B, C, or D.
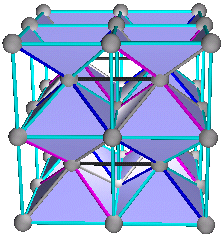
2. Combinations of A+B or C+D are the Simple Cubic (sc) structure or NaCl type structure. All of each others octahedra voids are filled. We have octahedral coordination, which is the alternative unit cells for simple cubic. A+B and C+D are two distinct simple cubic lattices that are topologically the same.
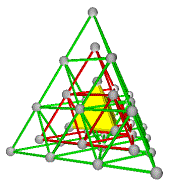
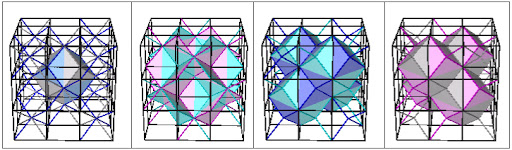
3. Combinations of A+C, B+C, A+D, or B+D are the cubic Diamond and related structures or ZnS structure. Half of each others tetrahedra are filled, A fills the negative tetrahedra of C and C fills the positive tetrahedra of A. We have tetrahedral coordination. There are four distinct diamond lattices that are topologically the same.
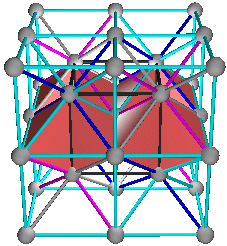
4. Combinations of A+(C+D), B+(C+D), (A+B)+C or (A+B)+D are the fluorite (AX2) CaF2 and the antifluorite (A2X) Na2O structures. Half of the (C+D) simple cubic are filled or all of A's or B's tetrahedra are filled, and half of the (A+B) simple cubic are filled or all of C's or D's tetrahedra are filled. It can also be seen as two interpenetrating diamond lattices like A+(C+D) as combination of diamond lattices (A+C) and (A+D).
5. Combinations of A+B+C+D are the body centered cubic structure. All tetrahedra and octahedra are filled, or (A+B)+(C+D) the CsCl structure (two simple cubic), (A+C)+(B+D) or (A+D)+(B+C) viewed as two interpenetrating diamond structures.
1. The Cubic Closest Packed Structure
A, B, C, or D
Elements: Al, Ca, Cu, Ni, Sr, Rh, Pd, Ag, (Ce), (Tb), Ir, Pt, Au, Pb, Th
See (Fig.5a, 5b, 5c, or 5d)
Compounds: Cu3Au, AlNi3 (others?). See (Fig. 20b) under Compound ccp lattice (Cu3Au)
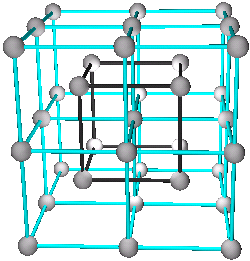
2. The Simple Cubic Structure or NaCl Structure
A+B or C+D
Elements: Alpha Po
Compounds: NaCl, AgCl, BaS, CaO, CeSe, DyAs, GdN, KBr, LaP, LiCl, LiF, MgO, NaBr, NaF, NiO, PrBi, PuC, RbF, ScN, SrO, TbTe, UC, YN, YbO, ZrO (Ref. 4)
 Fig. 6a. Combination A+B. 3 frequency simple cubic or 27 sc unit cells. A in red, and B in blue.
Fig. 6a. Combination A+B. 3 frequency simple cubic or 27 sc unit cells. A in red, and B in blue. Fig. 6b. Combination C+D. 2f or 8 unit cells. C in red, and D in blue.
Fig. 6b. Combination C+D. 2f or 8 unit cells. C in red, and D in blue.
3. The Cubic Diamond Structure or ZnS Structure
A+C, B+C, A+D, or B+D
Elements: C (diamond), Si, Ge, Sn (grey)
Compounds: ZnS, AgI, AlAs, AlP, AlSb, BAs, BN, BP, BeS, BeSe, BeTe, CdS, CuBr, CuCl, CuF, CuI, GaAs, GaP, GaSb, HgS, HgSe, HgTe, InAs, InP, MnS, MnSe, SiC, ZnSe, ZnTe (Ref. 4)
 Fig. 7a. Combination A+C. Diamond net (blue) interconnecting the A and C lattices.
Fig. 7a. Combination A+C. Diamond net (blue) interconnecting the A and C lattices.  Fig. 7b. Combination B+C. Diamond interconnecting net not shown.
Fig. 7b. Combination B+C. Diamond interconnecting net not shown.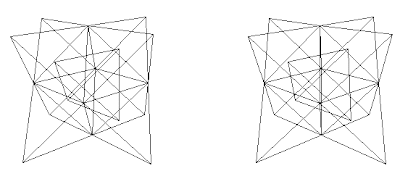
Fig. 7c. Combination A+D. Diamond interconnecting net in blue.
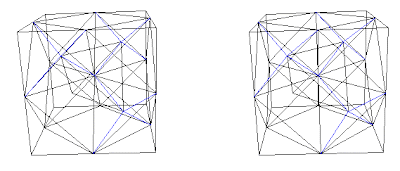
Fig. 7d. Combination B+D. Diamond interconnecting net in blue.
Fig. 7e. Diamond net, 4 unit cells. Traditional view. Combination A+C.
Fig. 7f. Diamond structure, same as (Fig. 7e). It is the combination A+C with A in blue. The interconnecting diamond net is not shown.
4. The Fluorite (AX2) and Antifluorite (A2X) Structures
A+(C+D), B+(C+D),
C+(A+B) or D+(A+B)
Elements: ? (There should be elements with this structure, unless this is an exception)
Compounds: CaF2,AmO2, AuAl2, AuIn2, BaF2, Be2B, CdF2, CeO2, CoSi2, EuF2, HgF2, Ir2P, Li2O, Na2O, NiSi2, PtAl2, Rb2O, SrCl2, SrCl2, SrF2, ThO2, ZrO2 (Ref. 4)
Fig. 8a. Traditional view of fluorite structures. CaF2 as shown on pg. 252 (Ref. 3) and pg. 52 (Ref. 5). This is a C+(A+B) combination, where Ca = (C) and F = (A+B) as shown in (Fig. 8b)
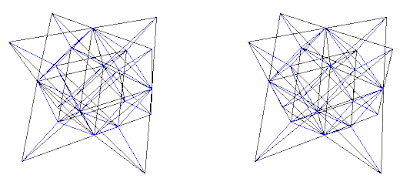
Fig. 8b. Combination C+(A+B). CaF2 shown in traditional view in blue with Ca = C lattice and F = (A+B) lattices. Cube outline is not shown.
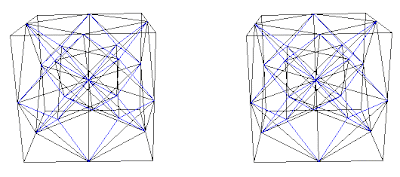
Fig. 8c. Combination D+(A+B) with interconnecting blue net.
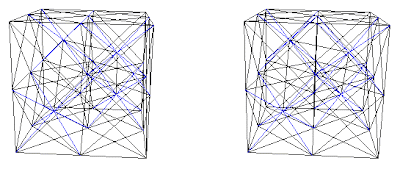
Fig. 8d. Combination A+(C+D) with interconnecting blue net.
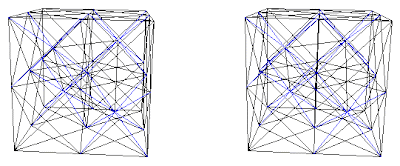
Fig. 8e. Combination B+(C+D) with interconnecting blue net.
Fig. 8f. Fluorite of 8 unit cells. They are cubic closest packed rhombic dodecahedra. This is a C+(A+B) view.
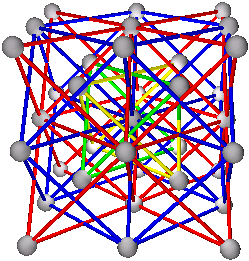
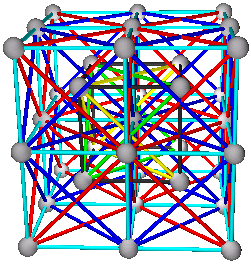
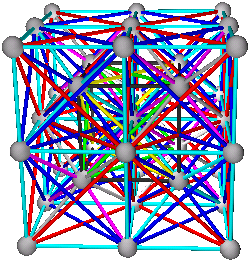
5. Body Centered Cubic Structures
A+B+C+D
(A+B)+(C+D)
(A+C)+(B+D) or (A+D)+(B+C)
Elements: W, Li, Na, K, V, Cr, Fe, Rb, Nb, Mo, Cs, Ba, Eu, Ta
Compounds:
- CsCl, CsBr, RbCl, AlCo, AgZn, BeCu, MgCe, RuAl, SrTl (Ref. 4)
- NaTl, LiZn, LiCd, LiAl, LiGa, NaIn, (pg 1301, Ref. 3)
- Fe3Al, Li3Bi, Li3Sb, Li3Pb, (pg 1301, Ref. 3)
- AlCu2Mn, AlNi2Ti, AlNi2Hf (Ref. 4)
CsCl has structure of type (A+B)+(C+D) with A=Cs, B=Cs, C=Cl, and D=Cl, or (Cs+Cs)+(Cl+Cl)

Fig. 9a. CsCl structure with traditional view.
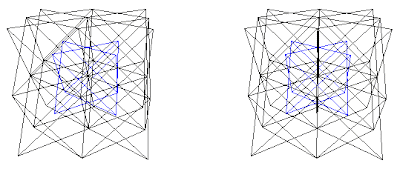
Fig. 9b. CsCl structure, (A+B)+(C+D). With (A+B) in blue.
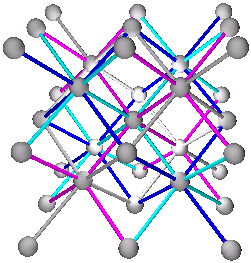
Fig. 9c. NaTl with combination of (A+B)+(C+D) as (Na+Tl)+(Tl+Na). Tl is shown in blue. Also shown is the partial tetrahedral axial view, or the two interpenetrating diamond view, or (A+C)+(B+D) view on the upper right corner.
The above is the same view as (Fig. 29.12), pg 1301 (Ref. 3).
The 2 interpenetrating diamond view of (A+C)+(B+D) (Ref. 4) or to view in 3D go to: The NaTl (B32) Structure
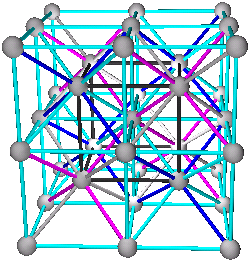
Fig. 9d. Fe3Al with combination of (A+B)+(C+D) as (Al+Fe)+(Fe+Fe) with Al shown in blue.
Same as shown in pg. 1298, fig. 29.10 (b) (Ref.3)
Cs3Sb has the same structure as Fe3Al with ((Cs/Sb)+Cs)+((Cs/Sb)+Cs) where (Cs/Sb) are equal numbers of Cs and Sb occupying sites A and C at random. From pg. 1301, (Ref. 3).
I just realized that the above coincides with Table 29.7, Structures of the CsCl-NaTl family, pg. 1302 (Ref. 3), in a way the atom positions Wells identified as A, B, C, and D corresponds exactly to the lattices A, B, C, and D used here. His chart includes in addition: Li3Bi, Bi2OF4, NaY3F10. Li3Bi shown in chart as A=Bi, B=Li, C=Li, D=Li it would translate to (A+B)+(C+D) as (Bi+Li)+(Li+Li) same as (Fig. 9d), Bi2OF4 shown in chart as A=4 Bi, (B,C,D)=2 O + 8 F, is not sufficient information to translate. NaY3F10 shown in chart as A=Na, 3 Y, (B, C, D)=10 F, from fig. 9.7, pg 422, translates to (A+B)+(C+D) as ((Na, 3 Y)+F)+(F+F) where Na occupies a tetrahedral vertex and 3 Y occupy the other three vertices of the tetrahedron.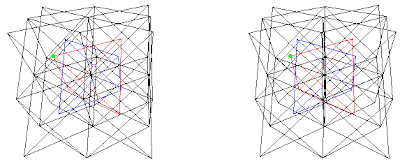
Fig. 9e. NaY3F10 in the combination (A+B)+(C+D) where Na in green and Y in red are A, F in blue is B, and F also occupy C and D lattices in black.
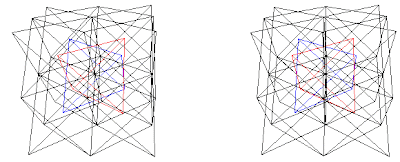
Fig. 9f. AlCu2Mn (A+B)+(C+D) (Al+Mn)+(Cu+Cu), Al is red and Mn is blue, from (Ref. 4) or to view in 3D go to: The Heusler (L21) Structure